符号定义

向下取整函数$\left\lfloor x \right\rfloor $定义为小于等于$x$的最大整数。
向上取整函数$\left\lceil x \right\rceil $定义为大于等于$x$的最小整数。
$\{ x\} $定义为实数$x$的小数部分，即
\[\{ x\} = x - \left\lfloor x \right\rfloor \]

性质

性质1

\[\left\lceil x \right\rceil - \left\lfloor x \right\rfloor = [x \in \mathbb{Z}]\]

性质2

取整函数范围：
\[x - 1 < \left\lfloor x \right\rfloor \le x \le \left\lceil x \right\rceil < x + 1\]

性质3

负数的取整：
\[\begin{array}{l}\left\lfloor { - x} \right\rfloor = - \left\lceil x \right\rceil \\\left\lceil { - x} \right\rceil = - \left\lfloor x \right\rfloor \end{array}\]

性质4

取整函数中的整数可以提取出来：
\[\left\lfloor {x + n} \right\rfloor = \left\lfloor x \right\rfloor + n\]

应用

应用1

证明：
\[\left\lfloor {\sqrt {\left\lfloor x \right\rfloor } } \right\rfloor = \left\lfloor {\sqrt x } \right\rfloor \]

更一般的，我们还可以证明，对于任意连续、递增的函数$f(x)$，如果它满足
\[f(x) \in \mathbb{Z} \Rightarrow x \in \mathbb{Z}\]
那么有
\[\begin{array}{l}\left\lfloor {f(x)} \right\rfloor = \left\lfloor {f(\left\lfloor x \right\rfloor )} \right\rfloor \\\left\lceil {f(x)} \right\rceil = \left\lceil {f(\left\lceil x \right\rceil )} \right\rceil \end{array}\]

我们证明第2个式子，第1个同理可证。

如果$x = \left\lceil x \right\rceil $，显然成立。

否则$x < \left\lceil x \right\rceil $，因为$f(x)$递增，所以有
\[f(x) < f(\left\lceil x \right\rceil )\]
两边同时取整，有
\[\left\lceil {f(x)} \right\rceil \le \left\lceil {f(\left\lceil x \right\rceil )} \right\rceil \]
要证左右两边相等，那么只要证
\[\left\lceil {f(x)} \right\rceil < \left\lceil {f(\left\lceil x \right\rceil )} \right\rceil \]
不成立即可。假设上式成立，那么由中间值定理，一定存在$x \le y < \left\lceil x \right\rceil $，使得
\[f(y) = \left\lceil {f(x)} \right\rceil \]
敲黑板！！这里是怎么来的呢？
由下图可以看出，当下面式子成立时，满足中间值定理
\[f(x) < \left\lceil {f(x)} \right\rceil < f(\left\lceil x \right\rceil )\]
但是在这里，我们假设是
\[\left\lceil {f(x)} \right\rceil < \left\lceil {f(\left\lceil x \right\rceil )} \right\rceil \]
那么由$\left\lceil {f(x)} \right\rceil < \left\lceil {f(\left\lceil x \right\rceil )} \right\rceil $能否推出$\left\lceil {f(x)} \right\rceil < f(\left\lceil x \right\rceil )$呢？当然是可以的。
\[\begin{array}{l}\left\lceil {f(x)} \right\rceil < \left\lceil {f(\left\lceil x \right\rceil )} \right\rceil \\ \Rightarrow \left\lceil {f(x)} \right\rceil \le \left\lceil {f(\left\lceil x \right\rceil )} \right\rceil - 1 < f(\left\lceil x \right\rceil )\end{array}\]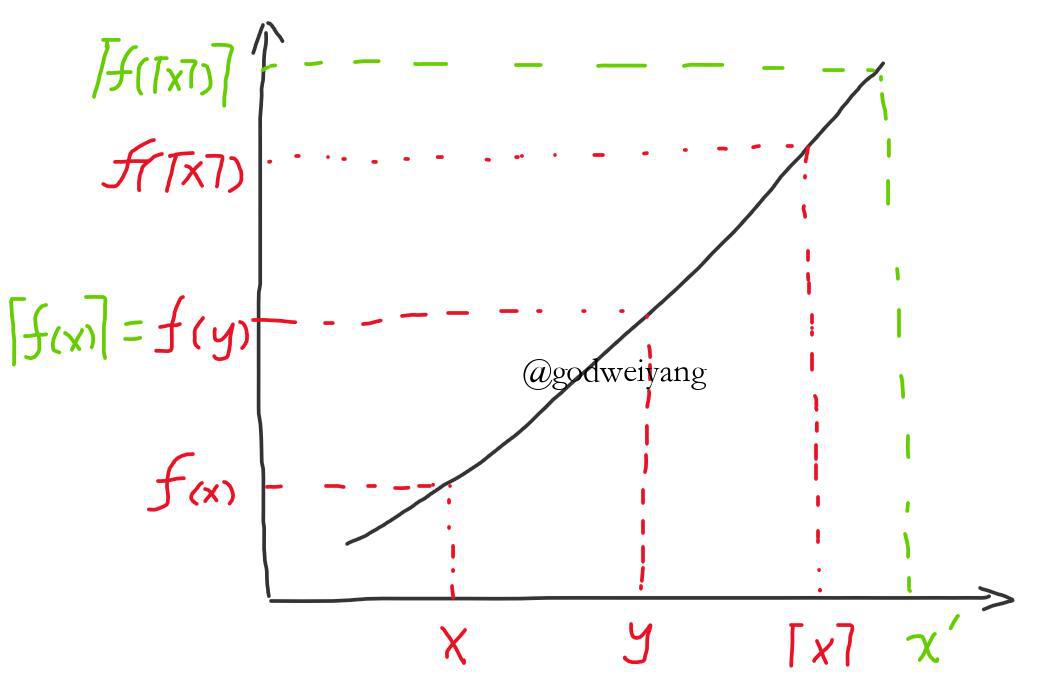

所以
\[f(y) \in \mathbb{Z} \Rightarrow y \in \mathbb{Z}\]
又因为$x \le y < \left\lceil x \right\rceil $，所以不存在整数$y$，矛盾！

所以证得
\[\left\lceil {f(x)} \right\rceil = \left\lceil {f(\left\lceil x \right\rceil )} \right\rceil \]

另一个特殊的例子是
\[\left\lfloor {\frac{ {x + m}}{n}} \right\rfloor = \left\lfloor {\frac{ {\left\lfloor x \right\rfloor + m}}{n}} \right\rfloor \]
其中$m$和$n$都是整数，并且$n$是正整数。

应用2

接着介绍区间相关的性质。

求1到1000中使得下列式子成立的$n$一共有多少个？
\[\left\lfloor {\sqrt[3]{n}} \right\rfloor |n\]
求解方法如下：
\[\begin{array}{l}W{\rm{ = }}\sum\limits_{1 \le n \le 1000} {\left[ {\left\lfloor {\sqrt[3]{n}} \right\rfloor |n} \right]} \\ = \sum\limits_{k,n} {\left[ {k = \left\lfloor {\sqrt[3]{n}} \right\rfloor } \right]\left[ {k|n} \right]\left[ {1 \le n \le 1000} \right]} \\ = \sum\limits_{k,m,n} {\left[ { {k^3} \le n < { {(k + 1)}^3}} \right]\left[ {n = km} \right]} \left[ {1 \le n \le 1000} \right]\\ = 1 + \sum\limits_{k,m} {\left[ { {k^3} \le km < { {(k + 1)}^3}} \right]} \left[ {1 \le k < 10} \right]\\ = 1 + \sum\limits_{k,m} {\left[ {m \in [{k^2},{ {(k + 1)}^3}/k)} \right]} \left[ {1 \le k < 10} \right]\\ = 1 + \sum\limits_{1 \le k < 10} {(\left\lceil { {k^2} + 3k + 3 + 1/k} \right\rceil - \left\lceil { {k^2}} \right\rceil )} \\ = 1 + \sum\limits_{1 \le k < 10} {(3k + 4)} \\ = 172\end{array}\]

继续推广，求1到$N$中使得上面式子成立的$n$有多少个？
令
\[K = \left\lfloor {\sqrt[3]{N}} \right\rfloor \]
也就是小于等于$\left\lfloor {\sqrt[3]{N}} \right\rfloor $的最大整数。
所以
\[\begin{array}{l}W = \sum\limits_{1 \le k < K} {(3k + 4)} + \sum\limits_m {\left[ { {K^3} \le Km \le N} \right]} \\ = \left\lfloor {N/K} \right\rfloor + \frac{1}{2}{K^2} + \frac{5}{2}K - 3\end{array}\]
渐进地等于
\[W = \frac{3}{2}{N^{2/3}} + O({N^{1/3}})\]

应用3

定义一个实数的谱为：
\[Spec(\alpha ) = \{ \left\lfloor \alpha \right\rfloor ,\left\lfloor {2\alpha } \right\rfloor ,\left\lfloor {3\alpha } \right\rfloor , \ldots \} \]

很容易证明如果两个实数$\alpha \ne \beta $，那么
\[Spec(\alpha ) \ne Spec(\beta )\]

假设$\alpha < \beta $，那么令
\[m(\beta - \alpha ) \ge 1\]
所以
$m\beta \ge m\alpha + 1 \Rightarrow \left\lfloor {m\beta } \right\rfloor > \left\lfloor {m\alpha } \right\rfloor $
所以集合$Spec(\beta )$中小于$\left\lfloor {m\alpha } \right\rfloor $的元素个数小于$m$。而集合$Spec(\alpha )$中小于$\left\lfloor {m\alpha } \right\rfloor $的元素个数大于等于$m$。所以两个集合不相等。

谱有很多奇妙的性质，例如下面两个谱：
\[\begin{array}{l}Spec(\sqrt 2 ) = \{ \left\lfloor {\sqrt 2 } \right\rfloor ,\left\lfloor {2\sqrt 2 } \right\rfloor ,\left\lfloor {3\sqrt 2 } \right\rfloor , \ldots \} \\Spec(2{\rm{ + }}\sqrt 2 ) = \{ \left\lfloor {2{\rm{ + }}\sqrt 2 } \right\rfloor ,\left\lfloor {2(2{\rm{ + }}\sqrt 2 )} \right\rfloor ,\left\lfloor {3(2{\rm{ + }}\sqrt 2 )} \right\rfloor , \ldots \} \end{array}\]
可以发现，这两个谱正好划分了正整数集。
证明方法也很简单，只要证明对任意正整数$n$，两个集合中小于$n$的元素个数之和为$n$，过程如下：
\[\begin{array}{l}\left\lfloor {k\sqrt 2 } \right\rfloor \le n\\ \Rightarrow k\sqrt 2 < n + 1\\ \Rightarrow k < \frac{ {n + 1}}{ {\sqrt 2 }}\end{array}\]
所以第一个集合中小于$n$的元素个数为
\[\left\lfloor {\frac{ {n + 1}}{ {\sqrt 2 }}} \right\rfloor \]
同理第二个集合中小于$n$的元素个数为
\[\left\lfloor {\frac{ {n + 1}}{ {2 + \sqrt 2 }}} \right\rfloor \]
所以总个数为
\[\begin{array}{l}\left\lfloor {\frac{ {n + 1}}{ {\sqrt 2 }}} \right\rfloor + \left\lfloor {\frac{ {n + 1}}{ {2 + \sqrt 2 }}} \right\rfloor \\ = \left\lfloor {\frac{ {\sqrt 2 }}{2}(n + 1)} \right\rfloor + \left\lfloor {\frac{ {2 - \sqrt 2 }}{2}(n + 1)} \right\rfloor \\ = n + 1 + \left\lfloor {\frac{ {\sqrt 2 }}{2}(n + 1)} \right\rfloor + \left\lfloor { - \frac{ {\sqrt 2 }}{2}(n + 1)} \right\rfloor \\ = n + 1 + \left\lfloor {\frac{ {\sqrt 2 }}{2}(n + 1)} \right\rfloor + \left\lfloor {\frac{ {\sqrt 2 }}{2}(n + 1)} \right\rfloor - 1\\ = n\end{array}\]
得证。