汉诺塔问题

这是个老生常谈的问题了，n个盘子，3个柱子的汉诺塔问题，最少移动次数记为$T(n)$。
那么\[T(n)=2T(n-1)+1\]
边界条件为$T(0)=0$。
解出\[T(n)=2^n-1\]
验证可以采用数学归纳法，这里就不多说了。

直线分割平面问题

这也是个高中问题了，n条直线最多分割平面为几部分，记为$L(n)$。
那么\[L(n)=L(n-1)+n\]
边界条件为$L(0)=1$。
解出\[L(n)=n(n+1)/2+1\]

这题有个扩展，n个V型最多分割平面为几部分？
解决思路如下：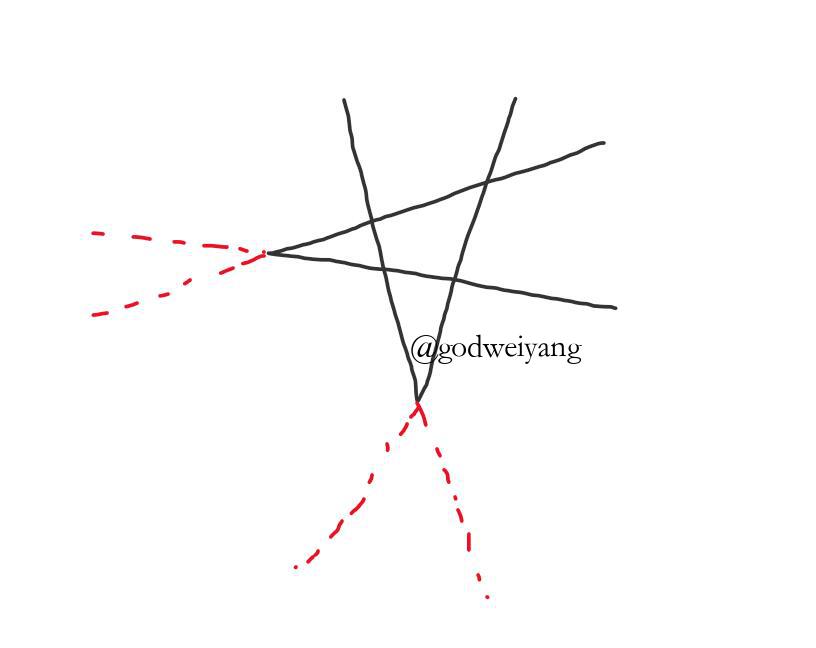

如上图所示，将V型补全（红色虚线部分），那么就转化为了$2n$条直线划分平面数，那么n个V型划分数只要减去$2n$就行了，所以答案为：
\[Z(n)=L(2n)-2n=2n^2-n+1\]

约瑟夫环问题

这个问题暴力求解的话模拟就行了，复杂度是$O(n^2)$的，这里探索一种直接求解的方法。
分两种情况讨论：
当有$2n$个人时，踢掉$n$个人之后，情况如下图所示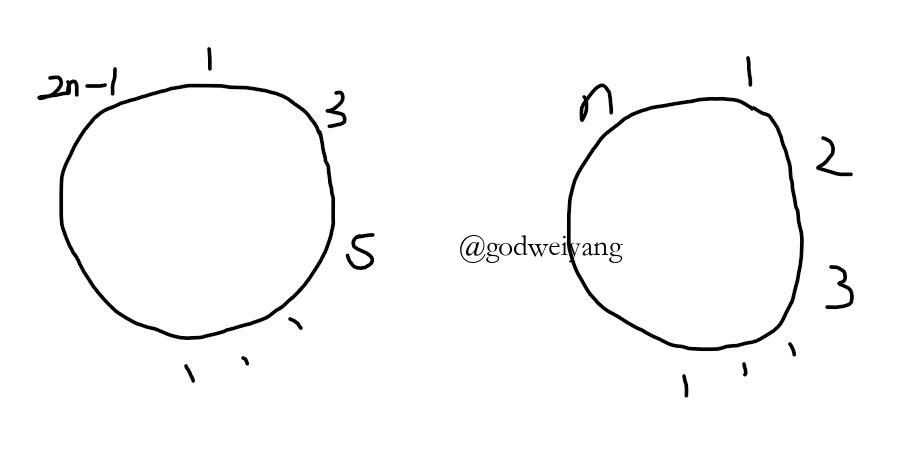

观察对应关系可以得出
\[J(2n)=2J(n)-1\]
同理，当有$2n+1$个人时，踢掉$n+1$个人之后，情况如下图所示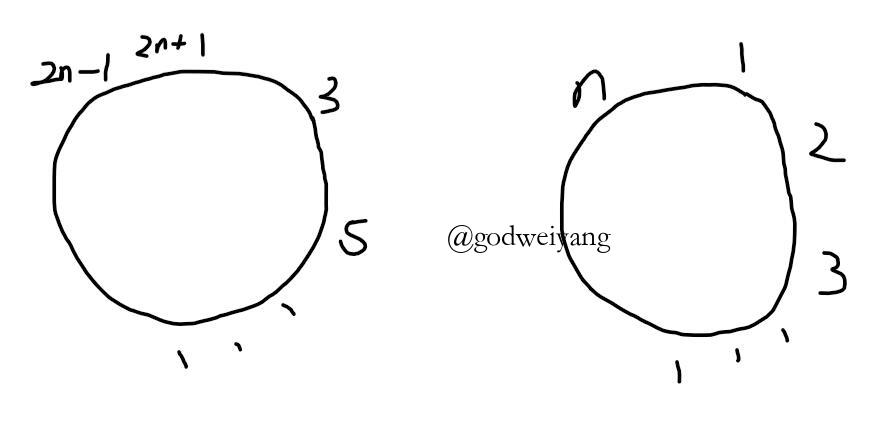

观察对应关系可以得出
\[J(2n+1)=2J(n)+1\]
边界条件为
\[J(1)=1\]
这个递推式很难求解，但是枚举出前面几项可以发现，如果令$n=2^m+l$，其中$2^m$是小于等于$n$的最大2的幂，那么
\[J(n)=2l+1\]
正确性可以通过数学归纳法求证。