关注公众号【算法码上来】,每日算法干货马上就来!
今天讲了多重求和,也就是一个和式由多个下标来指定。
首先是最简单的形式:
\[\sum\limits_{1 \le j,k \le n} { {a_j}{b_k}} = (\sum\limits_{1 \le j \le n} { {a_j}} )(\sum\limits_{1 \le k \le n} { {a_k}} )\]
例题1
下面给出一个对称矩阵:
\[A(i,j) = {a_i}{a_j}\]
求:
\[S = \sum\limits_{1 \le j \le k \le n} { {a_j}{a_k}} \]
这是这个矩阵的上三角加对角线求和,因为是对称的嘛,可以补全下三角,加上对角线就行了。
\[2S = \sum\limits_{1 \le j,k \le n} { {a_j}{a_k}} + \sum\limits_{1 \le j = k \le n} { {a_j}{a_k}} = {(\sum\limits_{1 \le k \le n} { {a_k}} )^2} + \sum\limits_{1 \le k \le n}^{} { {a_k}^2} \]
所以
\[S = \frac{1}{2}({(\sum\limits_{1 \le k \le n} { {a_k}} )^2} + \sum\limits_{1 \le k \le n}^{} { {a_k}^2} )\]
例题2
下面再看一个例子:
\[S = \sum\limits_{1 \le j < k \le n} {({a_j} - {a_k})({b_j} - {b_k})} \]
同样模仿上例调换$j,k$位置,得到:
\[\begin{array}{l}2S = \sum\limits_{1 \le j,k \le n} {({a_j} - {a_k})({b_j} - {b_k})} - \sum\limits_{1 \le j = k \le n} {({a_j} - {a_k})({b_j} - {b_k})} \\ = \sum\limits_{1 \le j,k \le n} {({a_j}{b_j} - {a_j}{b_k} - {a_k}{b_j} + {a_k}{b_k})} \\ = 2\sum\limits_{1 \le j,k \le n} { {a_j}{b_j}} - 2\sum\limits_{1 \le j,k \le n} { {a_j}{b_k}} \\ = 2n\sum\limits_{1 \le j \le n} { {a_j}{b_j}} - 2(\sum\limits_{1 \le j \le n} { {a_j}} )(\sum\limits_{1 \le k \le n} { {b_k}} )\end{array}\]
所以
\[S = n\sum\limits_{1 \le j \le n} { {a_j}{b_j}} - (\sum\limits_{1 \le j \le n} { {a_j}} )(\sum\limits_{1 \le k \le n} { {b_k}} )\]
至此解完,然后可以推出一个著名的不等式————切比雪夫不等式:
\[(\sum\limits_{1 \le j \le n} { {a_j}} )(\sum\limits_{1 \le k \le n} { {b_k}} ) = n\sum\limits_{1 \le j \le n} { {a_j}{b_j}} - \sum\limits_{1 \le j < k \le n} {({a_j} - {a_k})({b_j} - {b_k})} \]
如果
\[{a_1} \le {a_2} \le \cdots \le {a_n},{b_1} \le {b_2} \le \cdots \le {b_n}\]
那么
\[(\sum\limits_{1 \le j \le n} { {a_j}} )(\sum\limits_{1 \le k \le n} { {b_k}} ) \le n\sum\limits_{1 \le j \le n} { {a_j}{b_j}} \]
反之如果
\[{a_1} \le {a_2} \le \cdots \le {a_n},{b_1} \ge {b_2} \ge \cdots \ge {b_n}\]
那么
\[(\sum\limits_{1 \le j \le n} { {a_j}} )(\sum\limits_{1 \le k \le n} { {b_k}} ) \ge n\sum\limits_{1 \le j \le n} { {a_j}{b_j}} \]
更一般的结论,给定两个序列$a$和$b$,求下面式子最大值与最小值:
\[\sum\limits_{k = 1}^n { {a_k}{b_{p(k)}}} \]
其中$p(k)$是$\{ 1,2, \cdots ,n\} $的一个排列。
答案是$b$增序最大,降序最小,至于为什么,下面给出两种证明方法。
方法1
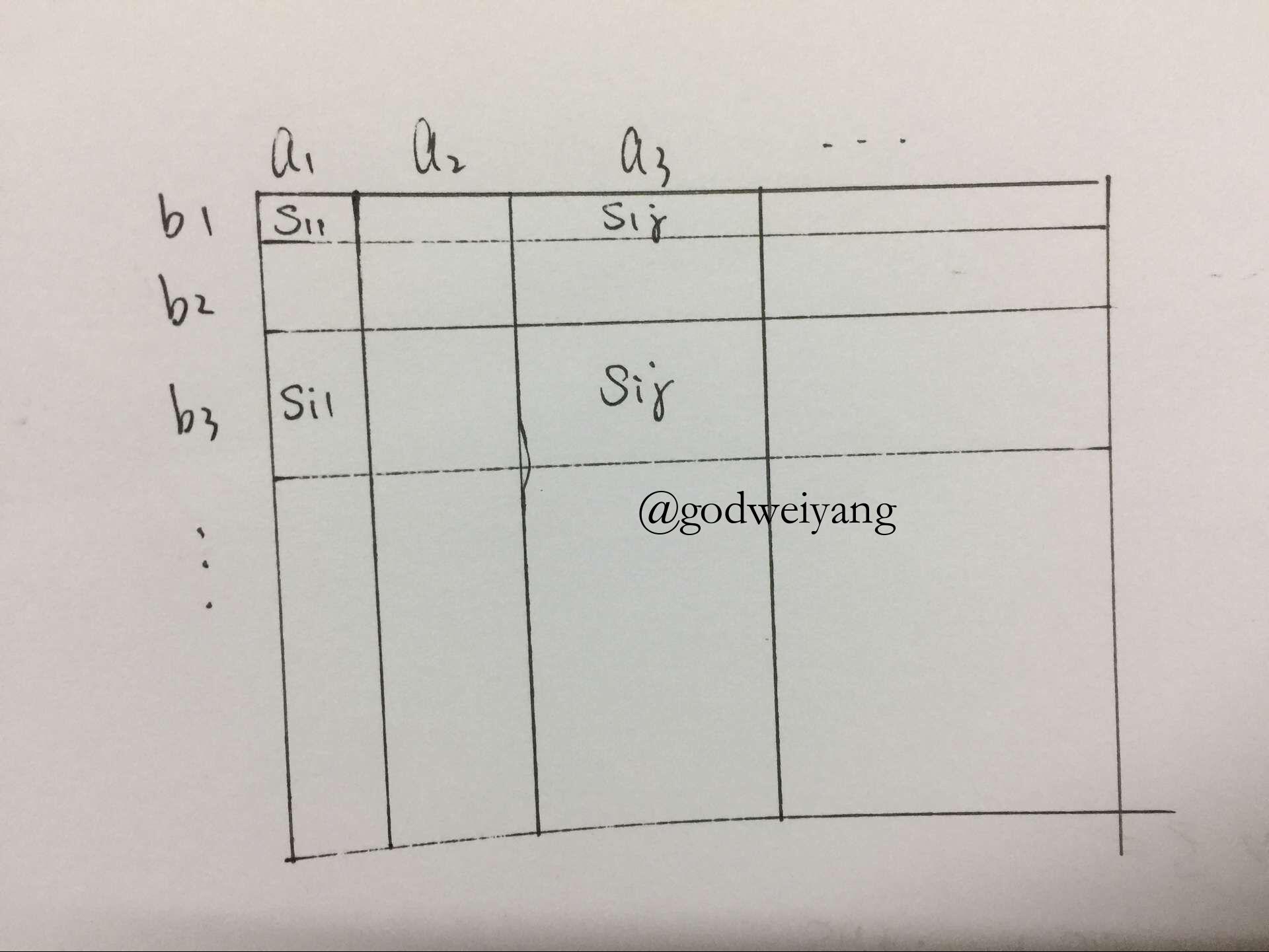
如上图所示,$a$和$b$按照递增顺序排列,每个方格的面积代表$a_i$与$b_j$的乘积,记为$s_{ij}$。
那么上面的求和式其实就是每一行每一列都必须有且只有一块被取。
考虑第一行,如果不取$s_{11}$,取其他的$s_{1j}$,那么第一列也只能取其他的$s_{i1}$,这样的话$s_{ij}$也就取不了了。但是发现
\[s_{11}+s_{ij} \ge s_{i1}+s_{1j}\]
并且两种取法影响的行和列都是相同的,这说明了,取$s_{i1}$和$s_{1j}$不如取$s_{11}$和$s_{ij}$。所以$s_{11}$必取,然后第一行第一列就不能取了。剩下的方阵用相同的方法可以得出必取$s_{22}, \cdots ,s_{nn}$,也就是主对角线。
同理最小取法用副对角线可以推出。
方法2
设数列$a$和$b$非单调递减,那么有如下证明:
\[\begin{array}{l}{S_k} = \sum\limits_{i = 1}^k { {b_i}} ,{ {S’}_k} = \sum\limits_{i = 1}^k { {b_{p(i)}}} \\ \Rightarrow {S_k} \le { {S’}_k}\\ \Rightarrow \\\sum\limits_{i = 1}^n { {a_i}{b_i}} = {S_1}{a_1} - {S_1}{a_2} + {S_2}{a_2} - {S_2}{a_3} + \cdots + {S_n}{a_n}\\ = \sum\limits_{i = 1}^{n - 1} { {S_i}} ({a_i} - {a_{i + 1}}) + {S_n}{a_n}\\ \ge \sum\limits_{i = 1}^{n - 1} { { {S’}_i}} ({a_i} - {a_{i + 1}}) + {S_n}{a_n}\\ = \sum\limits_{i = 1}^n { {a_i}{b_{p(i)}}} \end{array}\]
反之亦证。
题外话,其实切比雪夫不等式原来是以微积分形式给出的:
如果函数$f(x)$和$g(x)$非单调递减,那么有:
\[(\int_a^b {f(x)dx} )(\int_a^b {g(x)dx} ) \le (b - a)(\int_a^b {f(x)g(x)dx} )\]
例题3
求
\[S = \sum\limits_{1 \le j < k \le n} {\frac{1}{ {k - j}}} \]
我将用三种方法来求解这个式子。
方法1
首先将$j$和$k$分开,首先计算对$j$求和:
\[\begin{array}{l}S = \sum\limits_{1 \le k \le n} {\sum\limits_{1 \le j < k} {\frac{1}{ {k - j}}} } \\ = \sum\limits_{1 \le k \le n} {\sum\limits_{1 \le k - j < k} {\frac{1}{j}} } \\ = \sum\limits_{1 \le k \le n} {\sum\limits_{0 < j \le k - 1} {\frac{1}{j}} } \\ = \sum\limits_{1 \le k \le n} { {H_{k - 1}}} \\ = \sum\limits_{0 \le k < n} { {H_k}} \end{array}\]
方法2
先计算对$k$求和:
\[\begin{array}{l}S = \sum\limits_{1 \le j \le n} {\sum\limits_{j < k \le n} {\frac{1}{ {k - j}}} } \\ = \sum\limits_{1 \le j \le n} {\sum\limits_{j < k + j \le n} {\frac{1}{k}} } \\ = \sum\limits_{1 \le j \le n} {\sum\limits_{0 < k \le n - j} {\frac{1}{k}} } \\ = \sum\limits_{1 \le j \le n} { {H_{n - j}}} \\ = \sum\limits_{0 \le j < n} { {H_j}} \end{array}\]
方法3
按对角线求和:
\[\begin{array}{l}S = \sum\limits_{1 \le j < k \le n} {\frac{1}{ {k - j}}} \\ = \sum\limits_{1 \le j < k + j \le n} {\frac{1}{k}} \\ = \sum\limits_{1 \le k \le n} {\sum\limits_{1 \le j \le n - k} {\frac{1}{k}} } \\ = \sum\limits_{1 \le k \le n} {\frac{ {n - k}}{k}} \\ = n\sum\limits_{1 \le k \le n} {\frac{1}{k} - } \sum\limits_{1 \le k \le n} 1 \\ = n{H_n} - n\end{array}\]
由此得到了一个完全不同的表示形式!
所以我们得到了:
\[\sum\limits_{0 \le j < n} { {H_j}} = n{H_n} - n\]




