关注公众号【算法码上来】,每日算法干货马上就来!

本文不再更新,请移步最新第二版综述。
成分句法分析综述(第二版)
一直以来想对保研到现在一年多看过的论文进行一个总结,正好赶上下周二要讲组会,所以将自己看过的成分句法分析相关的论文梳理一下,写一个粗略的综述。可能有很多细节还不是很懂,理解有误,还请大家指正。
PPT地址:A Summary of Constituent Parsing
代码地址:Constituent Parsing
介绍
成分句法分析(constituent parsing)是自然语言处理中的一个基础任务,它的任务是给定一个句子,分析出句子的短语结构句法树。例如给定句子“The little boy likes red tomatoes .”,它的成分句法树如下图所示: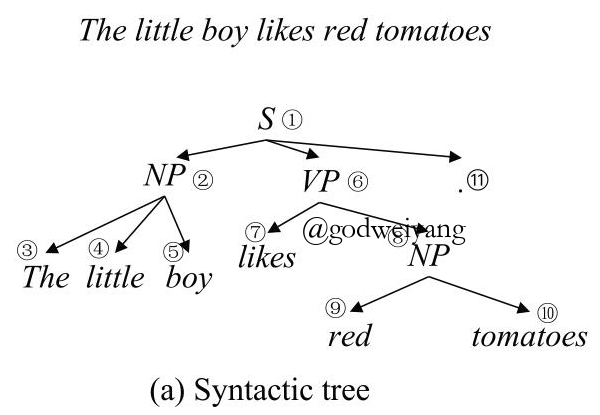
成分句法分析可以利用到许多下游任务中去,比如情感分析可以利用句子的成分句法树来进行递归神经网络建模,从而分析出句子的情感。也可以利用在其他基础任务中去,比如可以将训练好的成分句法树直接转为依存句法树,从而提升依存句法分析的准确率。
传统的成分句法分析方法主要是规则(grammar)和统计的,比如结合两者的概率上下文无关文法(PCFG),在此基础上产生了应用广泛的CKY解码算法。CKY算法本质上是一种动态规划算法,本文之后要讲到的chart-based模型的解码算法也是基于动态规划算法的,和CKY算法十分地相似。
Socher在2013年又提出了组合向量文法(CVG),将递归神经网络应用到了成分句法分析中,给每个短语结构赋予了向量表示。但是这种方法还是需要用到规则,采用CKY算法解码,时间效率比较低。还有一种基于CRF的神经网络句法分析方法,将离散的特征转化为了连续的特征表示。
不过,上面这些方法统统都不在本文的讨论范围之内。本文讨论近两年来研究最热门的几种模型,主要包括基于转移系统(transition-based)的模型、基于动态规划(chart-based)解码的模型、基于自顶向下贪心(greedy top-down)解码的模型和一些将预测树结构转化为预测序列(sequence to sequence)的模型。
基于转移系统的模型
基于转移系统的模型主要分为三大类。第一种是自底向上(bottom-up)的系统,代表性论文有Transition-based Neural Constituent Parsing等。第二种是自顶向下(top-down)的系统,代表性论文有Recurrent Neural Network Grammars和Span-Based Constituency Parsing with a Structure-Label System and Provably Optimal Dynamic Oracles等。最后一种是2017年提出的基于中序遍历(in-order)的系统,代表性论文有In-Order Transition-based Constituent Parsing等。
在这三类系统的基础之上,许多人又做了非常多的改进。例如提出了动态指导(dynamic oracle)技术,来解决序列预测中的exposure bias问题(具体含义之后会讲到)。还有使用强化学习中的policy gradient来代替dynamic oracle,解决了针对不同转移系统需要设计不同的dynamic oracle的问题。
基于转移的句法分析系统主要包含两个组成成分,一个是栈(stack),用来存放已分析的句法结构,另一个是缓存(buffer),用来存放待分析的句子。而预测句法树结构就转化为了预测转移系统每一个时刻应该采取的动作(action)序列。下面我们分别介绍几种不同的转移系统,我们用三元组$[S, B, T]$来表示转移系统每一个时刻的状态,分别代表栈、buffer的第一个单词下标、句法分析结束标志。
自底向上的转移系统
自底向上的转移系统是根据句法树的后序遍历(post-order)顺序进行句法分析的,首先将buffer中的单词移进栈里,然后将栈顶的若干个单词归约为它们的父结点,直至最后buffer为空并且栈里只有一个根节点。
在句法分析之前,首先要对句法树进行二叉化,这一点在传统的CKY算法中也会用到。例如对于之前的那棵句法树,二叉化后就变成了下图所示: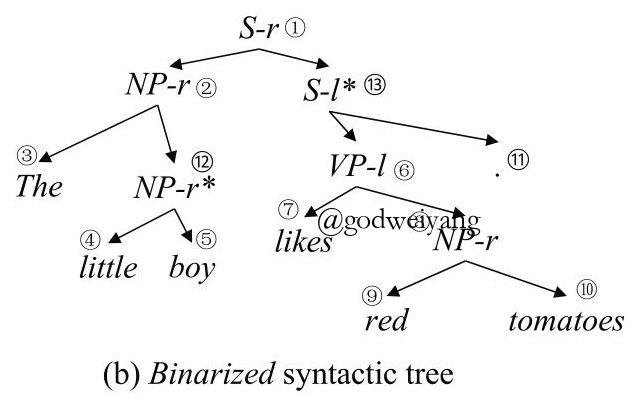
自底向上转移系统的action形式化定义如下: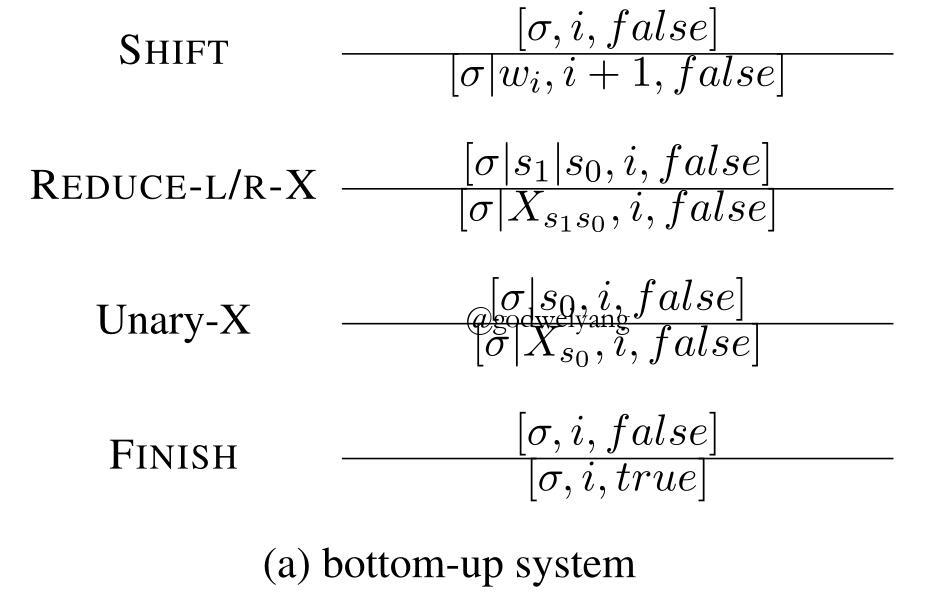
其中SHIFT动作就是将buffer里面的第一个单词移进栈里。REDUCE-L/R-X动作就是将栈顶的两个元素出栈,并且归约为它们的父结点X,然后再将父结点入栈,而L和R就是用来区分左儿子和右儿子谁是头结点(head branch)。Unary-X动作就是将栈顶元素出栈,并且归约为父结点X,这个动作是用来预测一元产生式的。最后FINISH动作用来判断句法分析是否结束。
注意到这里有一个问题:为什么这里一定要提前对句法树进行二叉化?主要原因是因为自底向上系统有个弊端,就是在不停地SHIFT之后,你不仅要预测哪一步开始REDUCE,还得预测REDUCE的话要REDUCE栈顶的多少个元素,这样预测的状态数就大大增加,导致训练时间也增加了许多。而二叉化后每次预测就只需要预测哪一步REDUCE就行了,每次REDUCE只REDUCE栈顶的两个元素。
对于上面的句法树,用自底向上系统分析的过程如下图所示: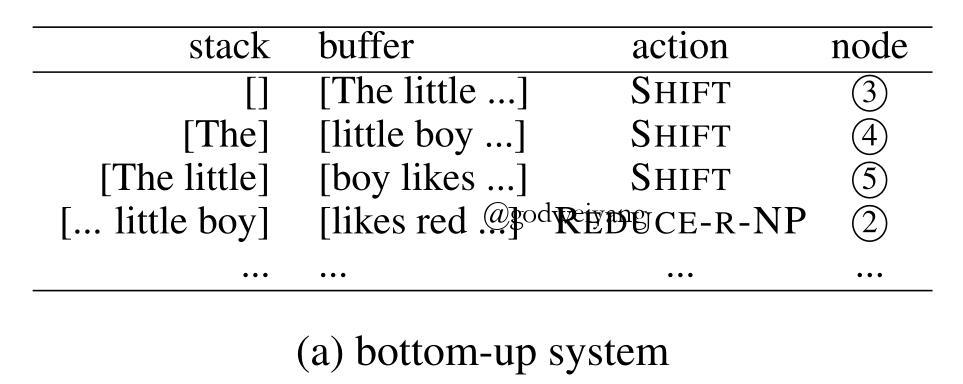
自底向上转移系统的优点就是可以充分利用已经生成的子树信息,来辅助后面的子树预测。
但是缺点也很显然,因为无法知道父结点以及再上层的父结点信息,所以丢失了许多有用的全局信息,这也有点类似于CKY算法的弊端了,同样只能根据局部的子树信息预测当前子树。
另一个缺点就是需要提前进行二叉化,虽然二叉化加入了head结点信息,事实证明是很有用的,但是head结点的标注需要许多语义学知识,也可以用神经网络来自己学习到head结点,但是二叉化总归是比较麻烦的。一个较为简洁的做法就是,用空结点$\emptyset$来作为本不应该归约的两个结点的临时结点,在还原树结构的时候忽略这种空结点,这样就可以隐式地进行二叉化操作了。
自顶向下的转移系统
自顶向下的转移系统利用的是句法树的前序遍历(pre-order)序列,首先将父结点入栈,然后不断操作直到它的子结点全部入栈,这时将父结点连同所有子结点全部归约为上一层的父结点。
自顶向下转移系统的action形式化定义如下:
其中SHIFT动作和之前一样,都是将buffer的第一个单词入栈。而NT-X动作就是将父结点X入栈。REDUCE动作就是将栈顶若干个元素直到它们的第一个父结点为止都出栈,然后归约为一个结点,再次入栈。注意到这里不同于自底向上系统的地方是没有FINISH动作,笔者也没有找到相关解释,猜测可能是因为自底向上系统存在一元动作Unary-X,所以最后根节点可能会无限归约下去,需要通过FINISH来提前终止分析。当然其实转移系统的动作定义并没有严格的要求,不同论文定义的也都不一样,但是都大同小异,也就是都存在SHIFT-REDUCE动作。
对于上面的句法树,用自顶向下系统分析的过程如下图所示: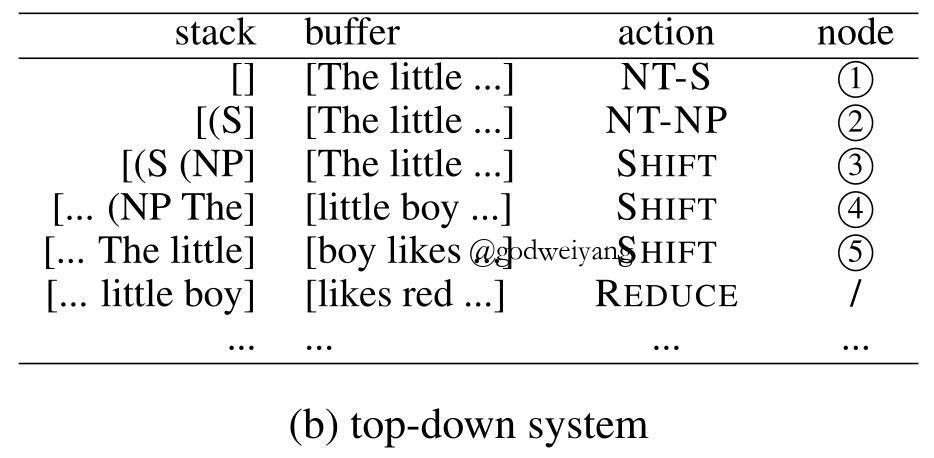
自顶向下系统的优缺点和自底向上系统恰好互补。优点就是可以充分利用全局信息,例如父结点的信息,并且不需要进行二叉化,因为REDUCE的时候只要往栈里找到第一个父结点就行了。而缺点就是无法利用局部信息,也就是子树信息,同样NT-X动作也可能会出现无限多次执行的情况,所以要加上一些限制条件。
In-order转移系统
Zhang和Liu两人在2017年提出了in-order转移系统,它利用的是句法树的中序遍历(in-order)序列,首先将一个子结点SHIFT入栈,然后将父结点入栈,再不断操作直到该父结点的剩余子结点全部入栈,然后对它们进行归约。
in-order转移系统的action形式化定义如下:
其中SHIFT动作和之前一样,都是将buffer的第一个单词入栈。PJ-X动作是预测出当前栈顶的元素的父结点X。REDUCE动作就是将栈顶的若干个元素归约为最里面倒数第二个元素,也就是它们的父结点。
对于上面的句法树,用in-order系统分析的过程如下图所示: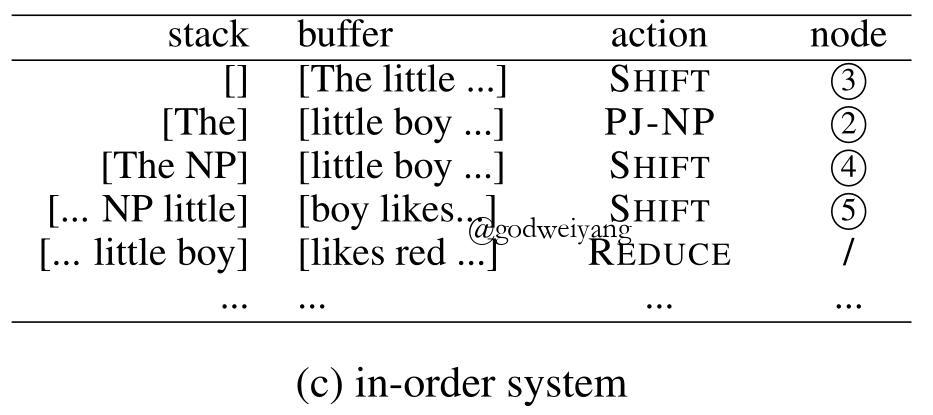
in-order转移系统提出的动机也很符合人类的直觉,在你读一个句子的时候,如果你第一个看到的单词是“The”,那么你脑海中可能会想到后面紧跟着的可能是个名词短语NP,然后你继续往后看,果然验证了你的猜想,后面的单词序列是“red tomatoes”。
in-order转移系统的优点恰好结合了前面两种转移系统,既可以考虑到局部信息,又可以考虑到全局信息。
模型变体:in-order系统就是在自顶向下系统的基础上,在父结点入栈之前先入栈了1个子结点。那么如果稍加修改,还可以提前入栈两个、三个等等。假设在父结点入栈之前先入栈了$k$个子结点,那么称这种转移系统为k-in-order系统。特别地,如果$k = 0$,那么这就是自顶向下转移系统;如果$k = 1$,那么这就是in-order转移系统;$k = \infty$,那么这就是自底向上转移系统。
模型框架
上面说到的三种基于转移的句法分析系统,都可以概括为预测每一个时刻的action,那么每一个时刻的状态如何表示就是最重要的问题。在每一个时刻,最重要的组成部分有三个,分别是当前栈的状态、当前buffer的状态、当前已生成的action序列的状态。
当前状态的表示通过下图所示的三个LSTM得到: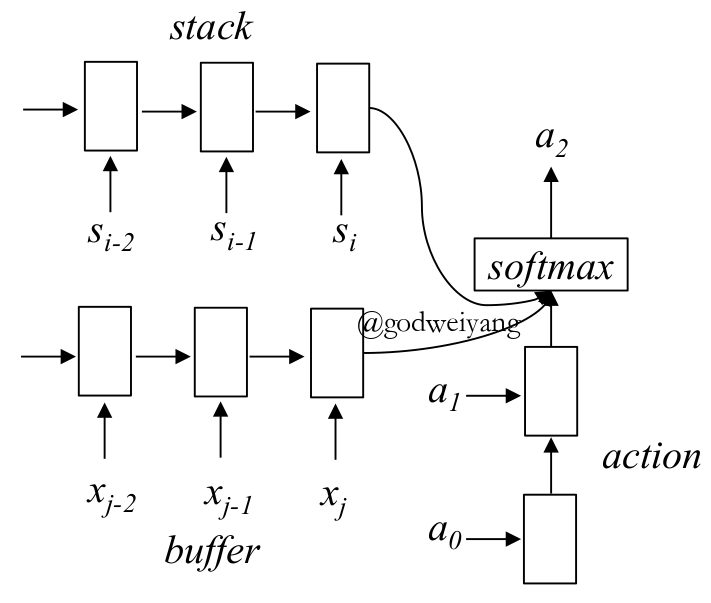
其中栈和buffer的编码使用的是stack-LSTM,而action的编码使用的是普通的LSTM。最后将三种LSTM输出拼接到一起,用softmax预测出正确的action。
另一个问题就是如何编码栈里的短语。在以前都是通过递归神经网络或者树状LSTM来编码树状结构短语的,而在这里的话直接将父结点和子结点合为一个序列,送入到双向LSTM中就行了,具体形式如下图所示: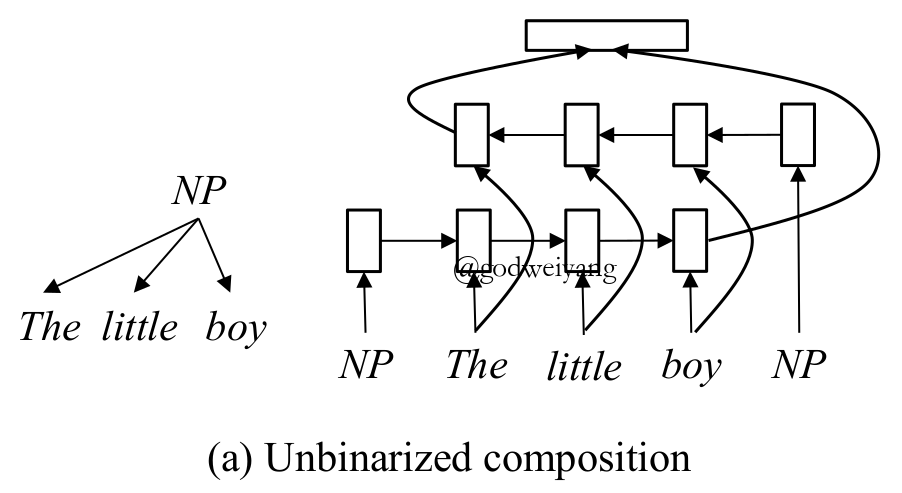
系统改进
基于span的自底向上的转移系统
黄亮在2016年论文里提出了转移系统的栈里用span的左右边界数值来代替分析出来的子树,并且将REDUCE动作和预测label分开来进行,他们的转移系统action形式化定义如下:
可以看出,在第偶数个时刻,只预测结构化动作sh和comb(对应于之前转移系统的SHIFT和REDUCE),sh动作从buffer中移进栈里一个单词$w_{j+1}$,栈顶的span就变为了$span(j, j+1)$。而comb动作就是将栈顶的两个span归约为一个span。在第奇数个时刻,只预测栈顶span的label,如果这个span的确能构成一个短语,那么就预测它的label,否则的话说明只是个临时结点,就预测为空结点,这一点在之前就已经提到过了。
论文里给出了一个具体的例子: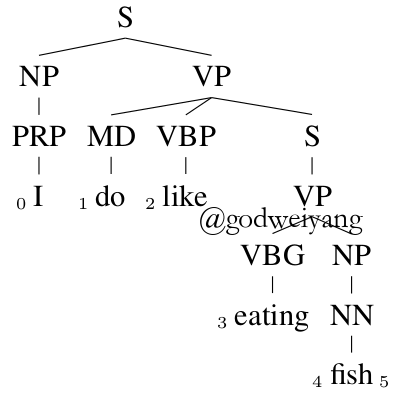
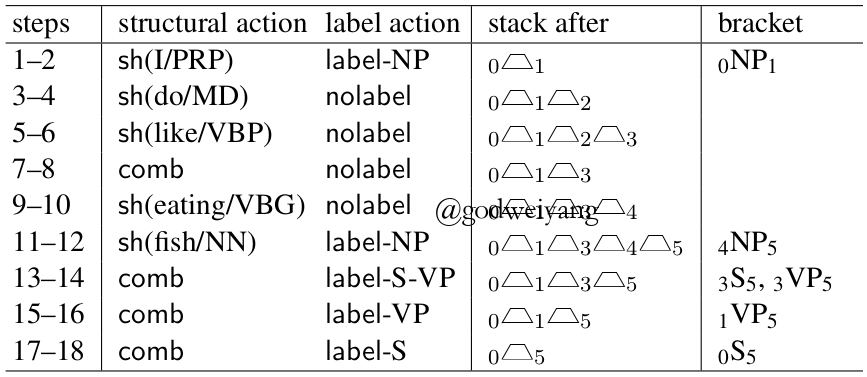
文章开头提供的代码也是基于这个转移系统的,一个好处是用span来表示的话比较方便,代码也好写。另一个好处就是每一个时刻的状态可以不再用三个LSTM动态地算出来了,而是可以提前用双向LSTM对句子进行编码,然后用两个单词输出的差值作为单词之间span的表示,最后用它来计算转移状态的向量表示。
例如在某个时刻,栈首元素为$(i, k, j)$,那么结构化预测就采用四个span特征:$span(0, i), span(i, k), span(k, j), span(j, n)$,为什么要用这四个呢?因为comb动作涉及到栈首的两个span,而之前已经生成的$span(0, i)$也可以作为局部信息指导预测,buffer中的$span(j, n)$也要考虑到,因为可能预测为sh动作,同时也可以作为全局信息参考。
而label预测就只要用到三个span特征:$span(0, k), span(k, j), span(j, n)$,因为label动作只需要对栈首的span进行预测,所以三个特征就足够了。
生成模型RNNG
RNNG是2016年提出的一种文法,全称叫做“Recurrent Neural Network Grammar”,是一种生成式模型。RNNG本质上就是自顶向下的转移系统,动作定义和之前介绍的基本一致。只是之前介绍的自顶向下的转移系统是判别式模型,每次SHIFT的单词都是buffer中给定的。而RNNG每次SHIFT的单词需要通过动作GEN(x)预测得出,最终模型对预测出来的句子分析出句法树。
正式一点就是,对于句子$x$和对应的句法树$y$,判别式模型是对条件概率$p(y | x)$进行建模,而生成式模型是对联合概率$p(x, y)$进行建模。
而RNNG的另一个重要应用是语言模型(language model),也就是建模$p(x)$。因为$p(x) = \sum\nolimits_{y \in \mathcal{Y}(x)} {p(x,y)}$,所以只需要枚举出所有可能的句法树$y$即可,但是这是指数级别的,显然不现实,这时候就需要用到“重要性采样(importance sampling)”。
令$q(y | x)$为RNNG作为判别式模型的时候产生句子$y$的条件概率,那么$p(x)$可以改写为
\[p(x) = \sum\nolimits_{y \in \mathcal{Y}(x)} {p(x,y)} = \sum\nolimits_{y \in \mathcal{Y}(x)} {q(y|x)w(x,y)} = {E_{q(y|x)}}w(x,y)\]
然后就可以采用蒙特卡罗方法进行采样了,从分布$q(y | x)$中采样$N$个样本:
\[{y^{(i)}} \sim q(y|x),i = 1,2, \ldots ,N\]
那么$p(x)$就可以近似表示为:
\[p(x) = {E_{q(y|x)}}w(x,y)\mathop \approx \limits^{MC} \frac{1}{N}\sum\limits_{i = 1}^N {w(x,{y^{(i)}})} \]
Dynamic Oracle
文章开头提到了一个转移系统会遇到的问题:“exposure bias问题”,这个问题意思就是训练的时候转移系统的每个时刻都是按照标准的action来进行训练的,但是如果测试的时候遇到了一个训练时从来没有遇见过的状态,这时候该怎么预测?如果预测错了,那么之后的时刻可能错的越来越离谱,偏差越来越大。
解决的方法就是采用Dynamic Oracle技术,在预测错误的时候,按照标准树的结构指导转移系统向着错误尽可能小的状态进行转移。但是比较麻烦的是,对于每一个转移系统,可能大家定义的状态都不尽相同,所以Dynamic Oracle要针对特定的转移系统单独设计,一个解决方法就是之后要提到的Policy Gradient方法。
这里举一个针对上面的“基于span的自底向上的转移系统”的Dynamic Oracle例子。
首先是结构化oracle,如果当前的栈首span是$span(i, j)$,那么就在标准树中寻找所有包含$span(i, j)$并且最小的span,记为$span(p, q)$,那么下一步可以采取的动作定义如下: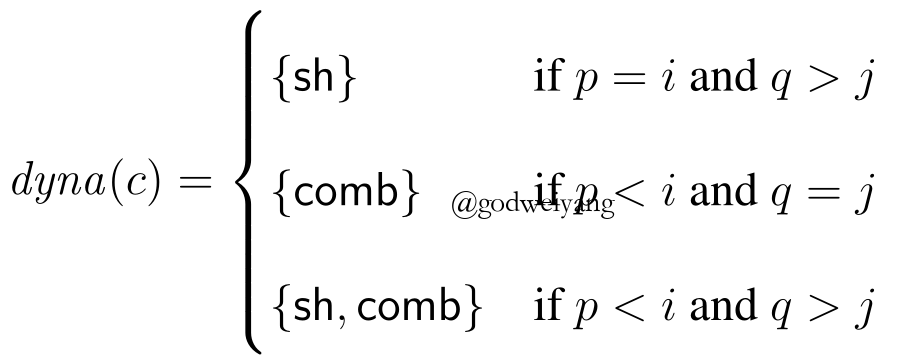
也就是说,如果$span(p, q)$比$span(i, j)$右边界多出一部分,那么为了向着标准span靠近,就只能sh单词入栈;否则如果左边界多出一部分,那么就必须先comb之前的两个span,扩大span左边的边界;否则的话左右两边都有空出,那就随机预测一个动作就行了。
然后是label oracle,这个就很简单了,如果当前的栈首span是$span(i, j)$,只需要在标准树中寻找是否存在$span(i, j)$,如果存在,那么就给他正常预测label就行了;如果不存在,那么直接预测为空结点。oracle定义如下: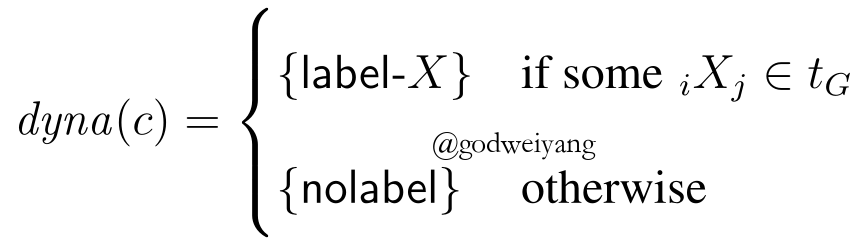
而关于这个Dynamic Oracle的证明和更加深入的理解,参见我之前写过的一篇博客:深入理解成分句法分析中的Dynamic Oracle。
但是如果直接按照这个Dynamic Oracle来实现代码的话,效果不会有什么提升,原因就是训练的时候遇到的错误情形还是太少了,不足以应付所有的测试阶段遇到的未知情形。所以要在训练阶段加上exploration操作,也就是转移的每一个时刻,不要总是预测概率最大的action,而是以一定的概率随机选择一个action,诱导系统进入一个错误的状态,这样系统就能学到更多错误状态下的回正技巧了。
Policy Gradient
序列预测存在着两个问题:一个就是之前提到的exposure bias问题,另一个就是loss mismatch问题,意思就是在每一个状态的loss累和得到最终整个序列的loss,但是因为是贪心解码,并没有考虑到之后的结果,所以某一个状态的loss其实并不能代表整个序列的loss。
Dynamic Oracle可以解决第一个问题,如果修改一下也可以解决第二个问题,但是Dynamic Oracle需要针对特定的转移系统单独设计,不能通用,所以这里引入了强化学习中的Policy Gradient来解决这个问题。
首先用风险函数(risk objective)代替原来的损失函数:
\[\mathcal{R}(\theta ) = \sum\limits_{i = 1}^N {\sum\limits_y {p(y|{x^{(i)}};\theta )\Delta (y,{y^{(i)}})} } \]
其中$(x^{(i)}, y^{(i)})$是训练集中的标准数据。可以看出,风险函数其实就是所有可能的句法树和标准树的差异${\Delta (y,{y^{(i)}})}$的期望,训练的目的就是最小化所有句法树和标准树的差异,这样就消除了之前提到的两个问题。
但是可以发现,显然不可能枚举所有可能的句法树,这时候想到了之前用到的重要性采样方法。
但是不能直接对风险函数进行重要性采样,不然就会发现采样后的函数$\theta$消失了!那就没办法求导了。所以先对风险函数求导:
\[\begin{array}{l}\nabla \mathcal{R}(\theta ) = \sum\limits_{i = 1}^N {\sum\limits_y {p(y|{x^{(i)}})\Delta (y,{y^{(i)}})\nabla \log p(y|{x^{(i)}};\theta )} } \\ \approx \sum\limits_{i = 1}^N {\sum\limits_{y \in \mathcal{Y}({x^{(i)}})} {\Delta (y,{y^{(i)}})\nabla \log p(y|{x^{(i)}};\theta )} } \end{array}\]
这里的$y$是根据分布${p(y|{x^{(i)}})}$采样得到的结果。实验中可以将标准树也加入到采样结果中,可以提升准确率。
至于$\log$项是怎么来的,可以如下推导得来:
\[\nabla p(y|{x^{(i)}};\theta ) = p(y|{x^{(i)}})\frac{ {\nabla p(y|{x^{(i)}};\theta )}}{ {p(y|{x^{(i)}};\theta )}} = p(y|{x^{(i)}})\nabla \log p(y|{x^{(i)}};\theta )\]
编码解码模型
上面介绍完了基于转移的句法分析系统,下面开始介绍编码解码(Encoder-Decoder)模型。
模型的大致框架如下图所示: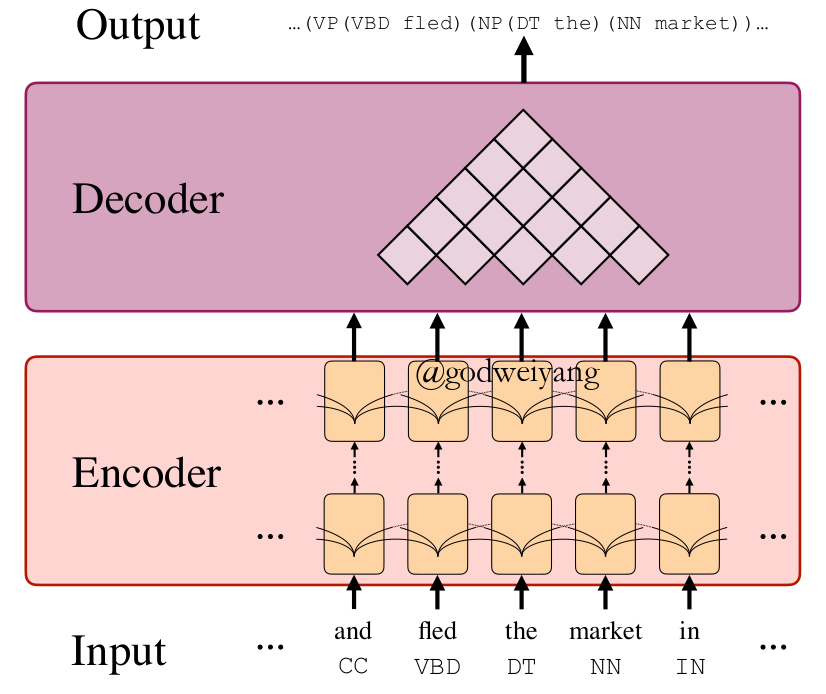
首先通过编码器将句子编码成向量,然后用解码器对向量操作,解码出句法树。
编码器(Encoder)
编码器的主要目的是将每个短语编码成语义向量,用来给解码器预测splits和labels。
编码器主要有两种,一种是简单的双向LSTM编码,下图是一个用双向LSTM对句子进行编码的示例: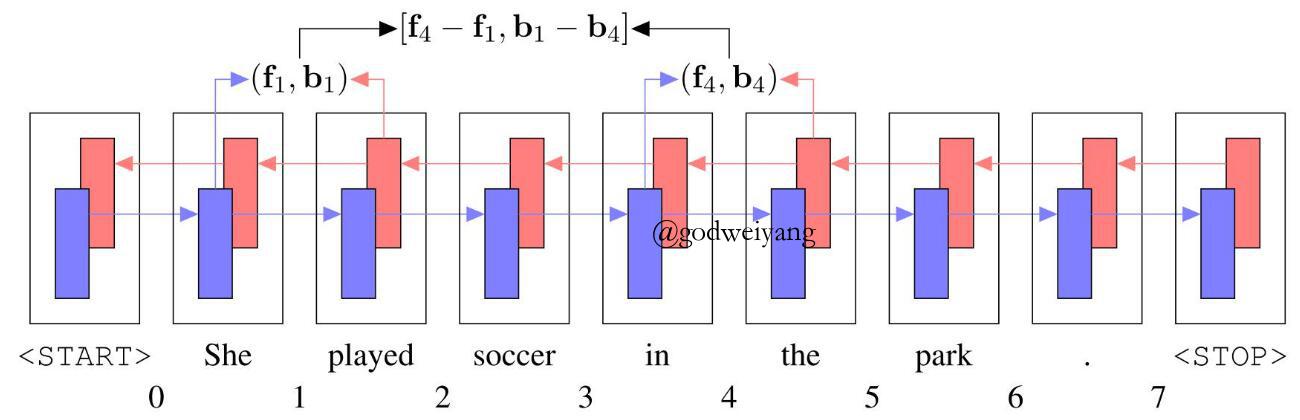
例如要编码“played soccer in”这个短语,那么就用“in”处的前向LSTM输出减去“She”处的前向LSTM输出,得到了短语的前向LSTM表示。类似的,用“played”处的反向LSTM输出减去“the”处的反向LSTM输出,得到了短语的反向LSTM表示。
另一种是multi-headed self-attention编码。Attention是谷歌在“Attention is all you need”中提出的一种方法,严格来说它并不能算作一种模型,只能说是一种机制。具体原理在这里就不细讲了,可以直接去看一下原文。
大体框架就是,每个单词的词向量经过三个不同的$W$矩阵变换之后得到了三个不同的向量表示$q, k, v$,分别拼接起来组成了矩阵$Q, K, V$,其中$Q, K$相乘就得到了任意两个单词之间的相似度矩阵,然后对矩阵每一行进行softmax就得到了每一个单词对于其他所有单词的权重。再乘上矩阵$V$就得到了它对其他所有单词的加权求和,以此来作为它的向量表示。
下图就是self-attention的框架图: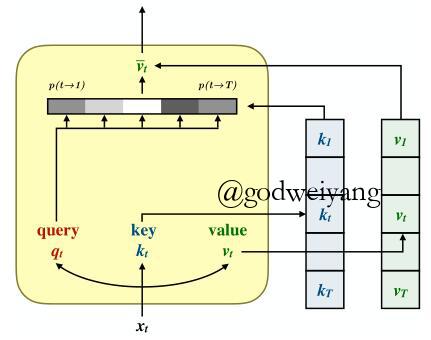
形式化定义就是:
\[S(X) = \left[ { {\rm{softmax}}\left( {\frac{ {Q{K^{\rm{T}}}}}{ {\sqrt { {d_k}} }}} \right)V} \right]{W_O}\]
其中$Q = XW_Q, K = XW_K, V = XW_V$,$d_k$是向量$q, k$的维度,用它作为分母是为了防止数值太大溢出。最后的矩阵$W_O$是为了将输出映射到与输入相同的维度。
而multi-headed self-attention就是将刚刚的attention计算8次,并且相加:
\[M(X) = \sum\limits_{i = 1}^8 {S(X)} \]
注意这8个attention的参数矩阵是不共享的,也可以不相加,改为直接拼接。
最终的编码器模型如下图所示: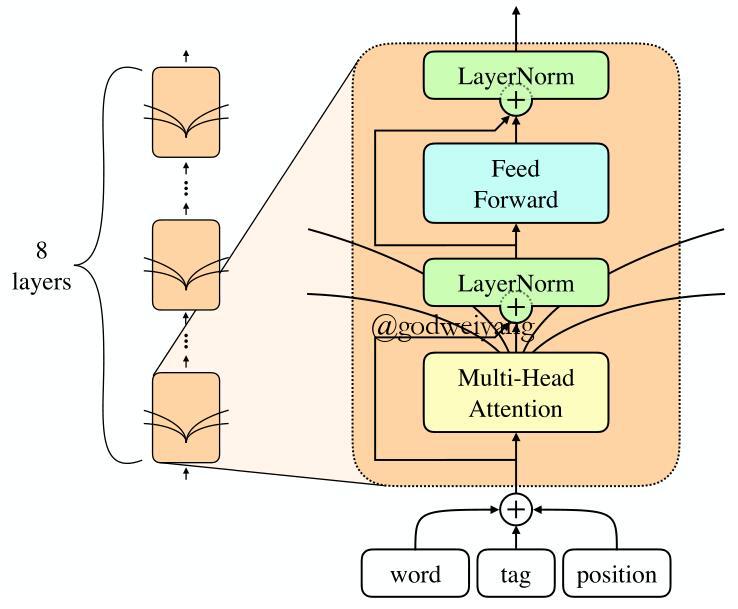
也就是说,将刚刚的multi-headed self-attention经过一层layernorm之后再经过一层前馈神经网络,最后再经过一层layernorm得到输出。将上述模型复制8份,首尾拼接,即前面的输出作为后面的输入,即可得到编码器最终的输出,也就是每个单词最终的向量表示。
至于每个短语的表示,和双向LSTM编码一样,用短语边界两个单词向量的差值作为短语的表示。只是这里没有前向后向的概念,所以要将每个单词向量一分为二,前一半作为前向向量,后一半作为后向向量。当然在实际实现中,将单数维度提取出来作为前向表示,双数维度提取出来作为后向表示。
解码器(Decoder)
得到了每个短语的向量表示之后,就需要对它们进行解码,得到最终的句法树,解码的方法主要有两种。
基于动态规划解码的模型
这种方法在论文中被叫做“chart-based model”,正如其名,就是利用一个数组来进行动态规划,求出每个span的最优split和最优label。
定义一棵句法树的分数为所有子结点的label分数之和,即:
\[{s_{tree}}(T) = \sum\limits_{(l,(i,j)) \in T} { {s_{label}}(i,j,l)} \]
其实原本论文中的定义还多了一项span的分数,但是由于具体实现中去掉这一项并没有什么影响,所以为了简便我就只算label分数了。
要使得句法树分数最大,不可能枚举所有的句法树,那就只能用动态规划算法求解了。对于任意一个$span(i, j)$,我们将它通过编码器产生的表示$s_{ij}$输入到前馈神经网络中,直接取得分最高的那一维作为最优label,即:
\[s_{label}(i, j, l) = [Vg(Ws_{ij}+b)]_l\]
而对于split,遍历所有的split,取两个子结点与自己结点得分之和最高的那个split即可:
\[s_{split}(i, j, k) = s_{label}(i, j, l_{ij}) + s_{label}(i, k, l_{ik}) + s_{label}(k, j, l_{kj})\]
最后的训练过程和以往一样,采用max-margin训练方法,即使得标准树的得分比预测树的得分至少高一个margin,在这里margin大小定义为两棵树不同短语的数量,最终的损失函数定义为:
\[\mathcal{L}(\theta ) = \max \left( {0,\Delta (\hat T,T) - {s_{tree}}(T) + {s_{tree}}(\hat T)} \right)\]
基于自顶向下贪心解码的模型
基于动态规划的解码算法时间复杂度为$O(n^3)$,对于长度大一点的句子来说还是有点不可接受的。但是如果采用自顶向下、贪心地去选择每一个span的最优split和最优label,那么时间复杂度将降到$O(n^2)$。具体操作过程如下,首先从根节点也就是$span(0, n)$开始,选择一个split,使得两个子结点与自己结点得分之和最高,而label还是向之前那样直接通过短语的向量计算得出。具体公式为:
\[\begin{array}{l}\hat l = \mathop {\arg \max }\limits_l [{s_{label}}(i,j,l)]\\\hat k = \mathop {\arg \max }\limits_k [{s_{split}}(i,k,l)]\end{array}\]
而由于贪心解码和转移系统action预测一样,在预测阶段可能会遇到训练阶段没有碰到过的状态,所以也需要用到Dynamic Oracle。同样也需要用到exploration,来增加训练阶段遇到的错误状态数。
Sequence to Sequence模型
上面最主流的两大模型:转移系统和编码解码模型都已经介绍完了,下面介绍几种比较新颖的方法。
大家都知道句法树和某些序列存在一一对应关系,句法树可以唯一转换成序列,序列也可以唯一转换成句法树,所以预测句法树的问题就转变为了预测序列问题,下面几种方法都是将句法树转换为了某种序列来进行预测。
树结构转化为括号序列
这种方法思路特别简单,因为训练集里原始数据的表示形式就是括号序列嘛,所以就采用语言模型直接预测出括号序列的概率。
但是不可能枚举出所有的句法树括号序列,所以最终还是只对其他句法分析器预测出来的最好的若干棵树进行预测概率,然后重排序选出概率最高的一棵树。
句法距离(Syntactic Distance)
这个方法就很新颖了,本质上也是将树结构转换成了唯一对应的序列。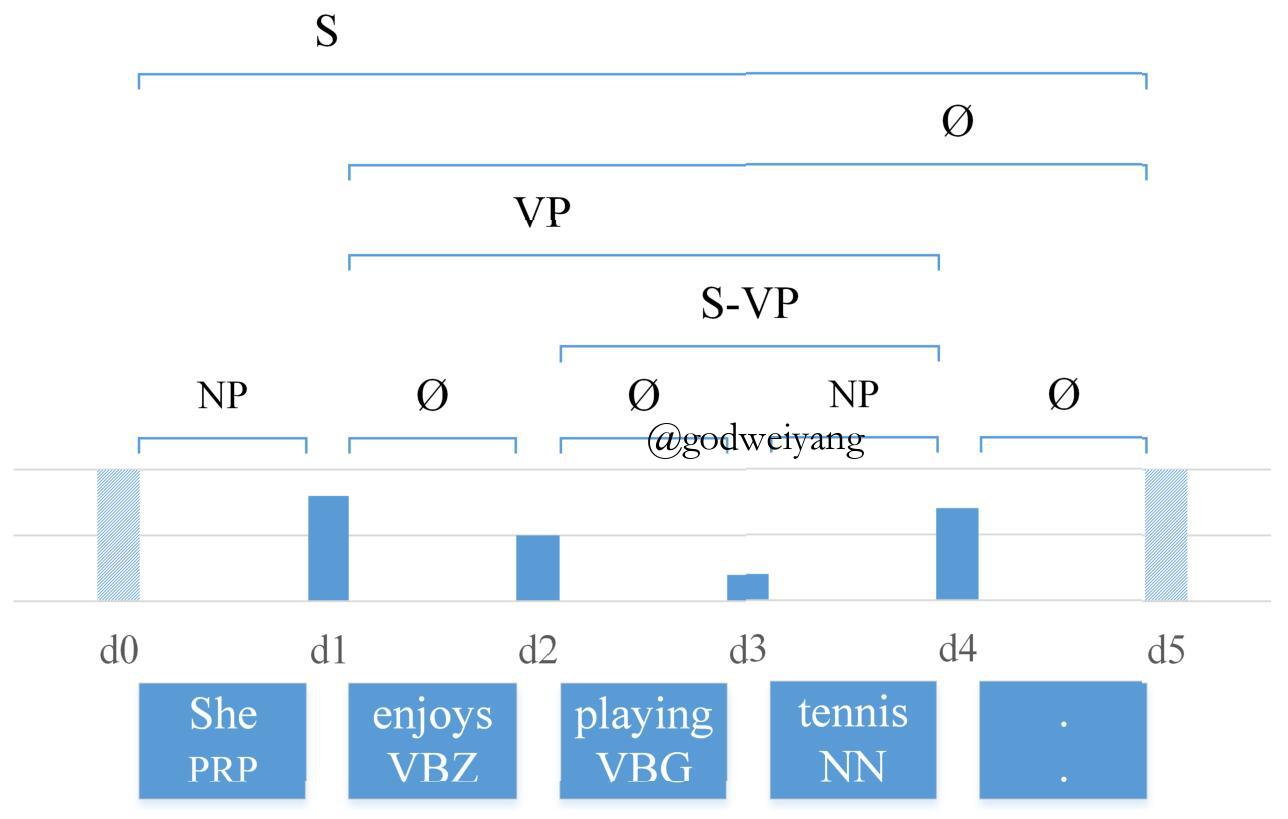
首先看上面一张图,对于长度为$n$的句子,存在一个长度为$n - 1$的数字序列,满足如下条件:$n$个单词存在$n - 1$个两两相邻的单词对,而两个相邻的单词的最近公共祖先(LCA)在句法树中有一个高度,所以这$n - 1$个数的大小关系恰好对应了从左向右任意两个相邻单词对的LCA的高度的大小关系。
拿上面那张图为例,“She”和“enjoys”的最近公共祖先是“S”,所以高度最高,对应的数字也最大。“enjoys”和“playing”的最近公共祖先是“VP”,高度排第三,所以对应的数字大小也是排第三。依次类推,剩下的数也满足这个性质。可以证明,这个数字序列和句法树是一一对应的。更进一步可以发现,这个序列其实就是“中序遍历的结点的高度”,文中将其称为句法距离。
预测这个序列也很简单,通过一个双向LSTM,然后将每相邻两个单词的输出做一次卷积操作(因为要预测相邻两个单词的LCA高度嘛),然后再将输出送到一个双向LSTM中去,最后通过一个前馈神经网络得到每相邻两个单词的数字。
而从树到序列和从序列到树的算法都很简单,这里就不详述了,可以直接去看论文。
总结
实验结果
下面列出了成分句法分析领域目前为止最好的一些结果: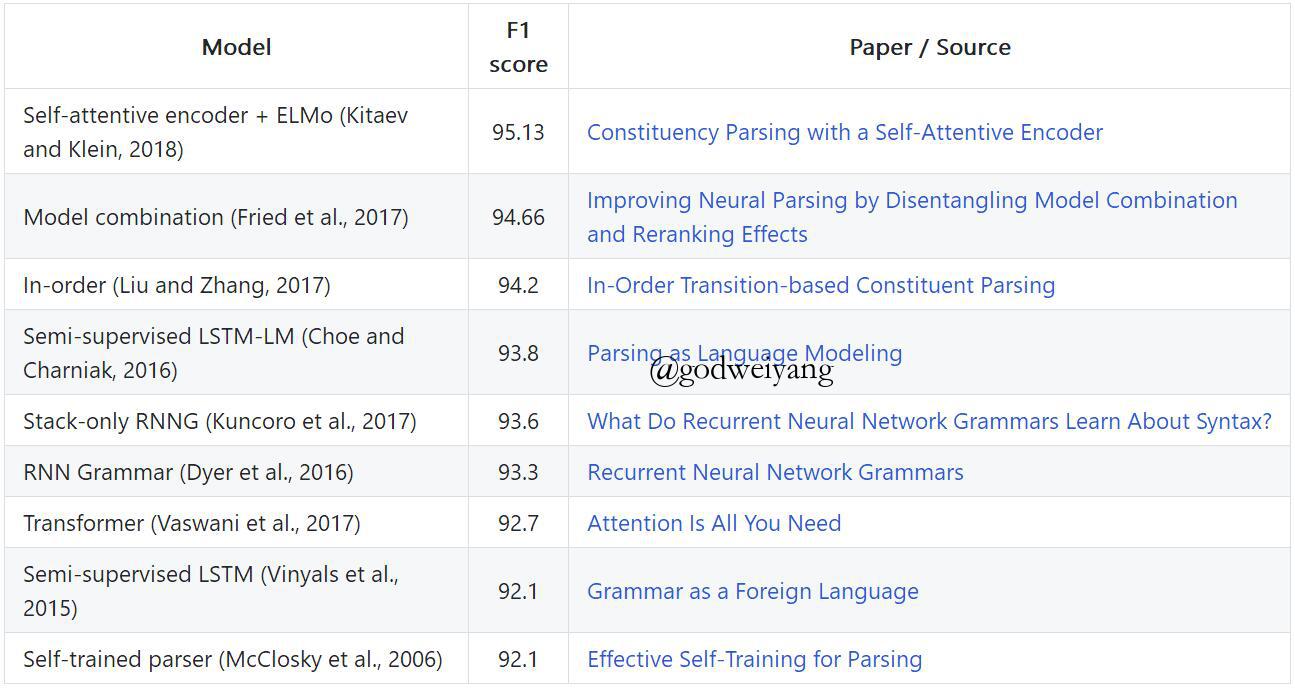
最好的是采用self-attention编码器+外部预训练词向量ELMo的模型,第二是模型融合+重排序之后的结果,之后的模型也基本都是本文介绍过的,最厉害的就是最后一个2006年的模型,十几年了依然如此强悍。
心得体会
虽然看起来貌似已经看了不少的成分句法分析相关的工作了,但是其实还有很多细节性的工作还没有去了解。前两年ACL等顶会成分句法分析的论文都很少,但是18年又好像多了起来,但终究还是伯克利Dan Klein、斯坦福Socher、黄亮等一批大佬在做这个,想在巨人的肩膀上面做出点东西还是很有挑战性的。
目前能想到的工作只有在编码器上面做文章,学习出语义更加丰富的短语表示。或者可以采用失传多年的递归神经网络,解码时对句法树进行建模,但是随便试了一下,速度很慢而且存在梯度消失的问题,效果也不是很好。转移系统的话暂时也想不出什么好的点子,序列预测的话如果能再想出个新颖的一一对应的序列就好了。
前路还很长,说长也不长了,只有三年不到的时间了,做不出东西就要延毕了。但愿能在有限的三年时间里做出点成果,提高自己的代码能力,对这个领域也有更加深入的理解!
参考文献
[ACL15] Transition-based Neural Constituent Parsing
[NAACL16] Recurrent Neural Network Grammars
[EMNLP16] Span-Based Constituency Parsing with a Structure-Label System and Provably Optimal Dynamic Oracles
[TACL17] In-Order Transition-based Constituent Parsing
[EMNLP17] Effective Inference for Generative Neural Parsing
[ACL18] Policy Gradient as a Proxy for Dynamic Oracles in Constituency Parsing
[ACL17] A Minimal Span-Based Neural Constituency Parser
[ACL18] Constituency Parsing with a Self-Attentive Encoder
[EMNLP16] Parsing as Language Modeling
[ACL18] Straight to the Tree: Constituency Parsing with Neural Syntactic Distance




