关注公众号【算法码上来】,每日算法干货马上就来!

inside-outside算法是用来预测一棵句法分析树的概率的算法,算法建立在文法是乔姆斯基范式(CFG)的基础之上,CFG的定义见维基百科。一棵句法分析树的potential定义为它包含的产生式的potential乘积,在PCFG中表示概率,在CRF-CFG中表示特征集合的分数。
inside-outside算法需要定义两个变量:
- $\alpha (A,i,j)$定义为内部的potential之和,即以$A$为根结点,短语为${x_{i;j}}$的所有可能的子树的potential之和。
- $\beta (A,i,j)$定义为外部的potential之和,即以$A$为根结点,短语为${x_{1;i - 1}}A{x_{j + 1;n}}$的所有可能的子结构的potential之和。
给定文法CFG,输入字符串${x_{1;n}}$,计算inside和outside值。
inside
初始化:
如果$A \to {x_i} \in R$,那么$\alpha (A,i,i) = \varphi (A \to {x_i},i,i,i)$。否则就等于0。
其中$\varphi (A \to {x_i},i,i,i)$为potential值。
类似于CKY算法,自底向上计算inside值:
\[\alpha (A,i,j) = \sum\limits_{A \to BC \in R} {\sum\limits_{k = i}^{j - 1} {\varphi (A \to BC,i,k,j) \cdot \alpha (B,i,k) \cdot \alpha (C,k + 1,j)} } \]
outside
初始化:
$\beta (S,1,n) = 1$,其余都等于0。
outside值要分为两部分计算: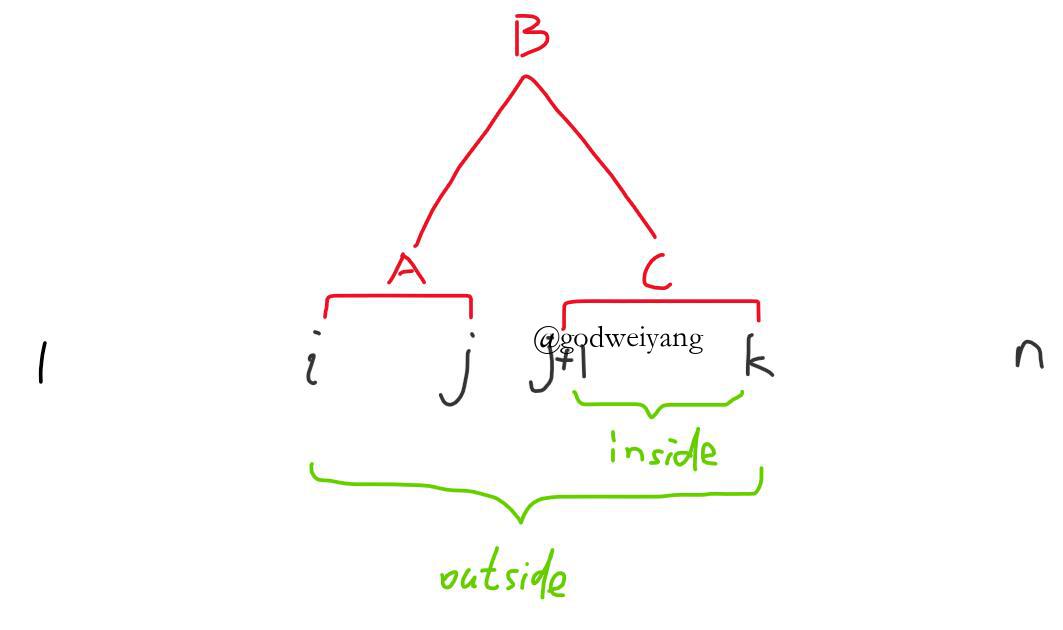
第一部分是${B \to AC}$,如上图所示。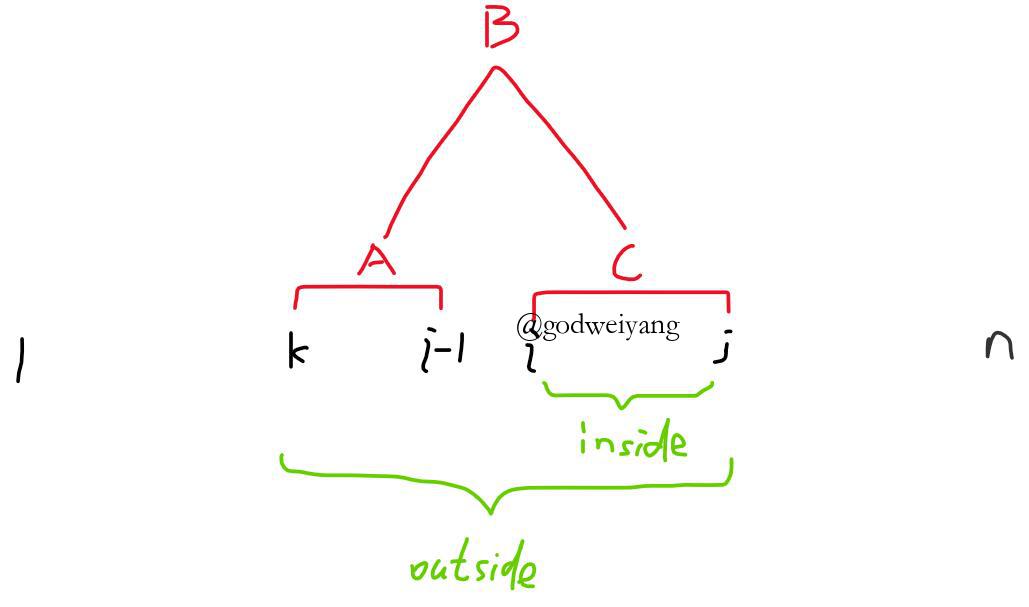
第二部分是${B \to CA}$,如上图所示。
和inside相反,通过自顶向下计算outside值:
\[\begin{array}{l}\beta (A,i,j) = \sum\limits_{B \to AC \in R} {\sum\limits_{k = j + 1}^n {\varphi (B \to AC,i,j,k) \cdot \beta (B,i,k) \cdot \alpha (C,j + 1,k)} } \\ + \sum\limits_{B \to CA \in R} {\sum\limits_{k = 1}^{i - 1} {\varphi (B \to CA,k,i - 1,j) \cdot \beta (B,k,j) \cdot \alpha (C,k,i - 1)} } \end{array}\]
应用
所有可能的句法树potential之和为:
\[{Z_s} = \alpha (S,1,n)\]
包含产生式$(A \to BC,i,k,j)$的所有可能句法树potential之和是:
\[\mu (A \to BC,i,k,j) = \varphi (A \to BC,i,k,j) \cdot \beta (A,i,j) \cdot \alpha (B,i,k) \cdot \alpha (C,k + 1,j)\]
存在非终结符$A$,且短语是${x_{i;j}}$的所有可能句法树potential之和是:
\[\mu (A,i,j) = \alpha (A,i,j) \cdot \beta (A,i,j)\]
PCFG参数估计
参数估计的目的就是为了估计出PCFG的概率$P$,使得所有句子的概率之和最大,采用的是EM迭代法。
首先定义:
\[\varphi (A \to BC,i,k,j) = P(A \to BC)\]
这里$P(A \to BC)$是随机初始化的,满足归一化条件就行。
对于语料库的每一条句子,可以计算出:
\[\begin{array}{l}count(A \to BC) = \frac { {\sum\limits_{i,k,j} {\mu (A \to BC,i,k,j)} }}{ { {Z_s}}}\\P(A \to BC) = \frac{ {count(A \to BC)}}{ {\sum\limits_r {count(r)} }}\end{array}\]
然后算出期望,更新概率,迭代就行了。
CRF-CFG参数估计
首先定义:
\[\varphi (A \to BC,i,k,j) = \exp \sum\limits_t { {\theta _t}{f_t}(A \to BC,i,k,j)} \]
其中$f_t$为特征函数。
那么我们的目的就是训练特征参数$\theta$。
然后定义似然函数为
\[L(D;\theta ) = \sum\limits_{(t,s) \in D} {\left( {\sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s) - {Z_s}} } } \right)} + \sum\limits_i {\frac{ {\theta _i^2}}{ {2{\sigma ^2}}}} \]
求偏导为
\[\frac{ {\partial L(D;\theta )}}{ {\partial {\theta _i}}} = \sum\limits_{(t,s) \in D} {(\sum\limits_{r \in t} { {f_i}(r,s)} - {E_\theta }[{f_i}|s])} + \frac{ { {\theta _i}}}{ { {\sigma ^2}}}\]
这里可能有人看不懂,似然函数和偏导是怎么来的呢?下面我详细写一下过程。
似然函数:
\[\begin{array}{l}L(D;\theta ) = \sum\limits_{(t,s) \in D} {\log \frac{ {\exp \sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } }}{ {\sum\limits_{t \in T(s)} {\exp \sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } } }}} + \sum\limits_i {\frac{ {\theta _i^2}}{ {2{\sigma ^2}}}} \\ = \sum\limits_{(t,s) \in D} {\left( {\sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } - \log \sum\limits_{t \in T(s)} {\exp \sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } } } \right)} + \sum\limits_i {\frac{ {\theta _i^2}}{ {2{\sigma ^2}}}} \\ = \sum\limits_{(t,s) \in D} {\left( {\sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } - {Z_s}} \right)} + \sum\limits_i {\frac{ {\theta _i^2}}{ {2{\sigma ^2}}}} \end{array}\]
所以偏导为:
\[\frac{ {\partial L(D;\theta )}}{ {\partial {\theta _i}}} = \sum\limits_{(t,s) \in D} {\left( {\sum\limits_{r \in t} { {f_i}(r,s)} - \frac{ {\partial \left( {\log \sum\limits_{t \in T(s)} {\exp \sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } } } \right)}}{ {\partial {\theta _i}}}} \right)} + \frac{ { {\theta _i}}}{ { {\sigma ^2}}}\]
而
\[\begin{array}{l}\frac{ {\partial \left( {\log \sum\limits_{t \in T(s)} {\exp \sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } } } \right)}}{ {\partial {\theta _i}}}\\ = \frac{ {\sum\limits_{t \in T(s)} {\left( {\left( {\exp \sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } } \right) \cdot \sum\limits_{r \in t} { {f_i}(r,s)} } \right)} }}{ {\sum\limits_{t \in T(s)} {\exp \sum\limits_{r \in t} {\sum\limits_i { {\theta _i}{f_i}(r,s)} } } }}\\ = {E_\theta }[{f_i}|s]\end{array}\]
所以偏导就是这么来的。




